Project Introduction

      This project is about a dynamic simulation of multi-body mechanical systems in generalized coordinates involving friction, impacts, and external forcing using Mathematica.

  System Introduction

      This system is a system about a pendulum hits a plate. There is an impact when the pendulum hits the plate, and I draw a line on the plate to see its rotation. The external force is the friction of the ground.

In this system, when the pendulum hits the plate, the plate starts to run and the pendulum stops moving, because the pendulum transfers energy to the ball. Then, with the friction of the ground, the velocity of the plate decreases to zero.

      The following image shows the system.

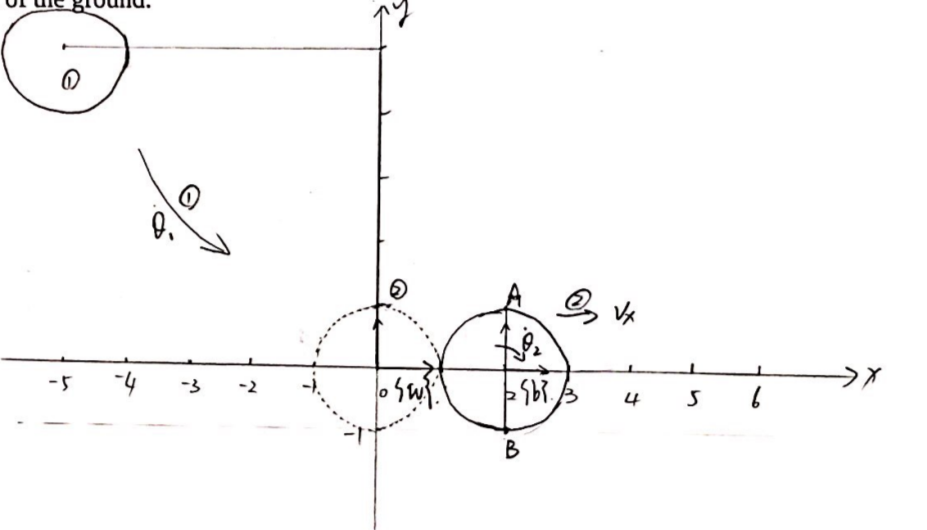
  Details

      (1). In the impact part, I use the angle(theta1) of the pendulum and (x,y) coordinates of center of mass of the plate to calculate Euler-Lagrange equation. The constraints are: 1). x always equals to 2; 2). y always equal to 0. The impact constrain is the distance between two centers: when the distance equals 2R, the pendulum hits the plate.

      (2). In the rotation part, I use inertia matrix and body velocity of the plate to calculate Euler-Lagrange equation, which relates to theta2(the angle that the plate rotate) and (x,y) coordinates of center of the plate. And the constraints are: 1). y always equals to zero; 2). theta times radius equals the distance the plate move.

      (3). The external forces is the friction of the ground, and I set the friction coefficient equals 0.4.